Glossário

Axiomas
1. Princípios ou regras que não são demonstrados e que disciplinam a utilização dos conceitos primitivos e estabelecem suas propriedades.
2. Postulados.

Completude dos reais
1. continuidade dos números da reta real.
2. Para Cantor, toda seqüência de números reais convergente tem limite, ou seja, o limite é um número real.
3. Para Dedekind, a completude da reta está no fato de que toda vez que “cortamos” a reta em dois pedaços A e B existe um ponto que P que produz tal “corte” e a separa em duas partes. O ponto P é associado a um número real.

Conceito primitivo
Conceito que não é definido, como por exemplo o de número e o de ponto.

Corolário
Proposição que é uma conseqüência de um teorema.

Corpo
Um conjunto numérico é um corpo, com relação a duas operações, “+” e “.”, quando: + é comutativa, associativa, tem elemento neutro 0 e todo elemento x do conjunto tem o seu oposto (-x), no conjunto, tal que x + (-x) = 0; “.” é comutativa, associativa, tem elemento


Os conjuntos dos Racionais, dos Reais e dos Complexos são corpos com relação à adição e à multiplicação.

Correspondência biunívoca
1. Função bijetora.
2. É uma correspondência entre dois conjuntos A e B tal que para cada (e para todos) elemento(s) de A existe um e só um elemento corresponde em B.

Demonstração
Sucessão de argumentos restritos às regras da lógica mostrando que determinada afirmação é necessáriamente verdadeira quando se assumem certos elementos primitivos e certos axiomas.

Eudoxo
Matemático grego que, por volta de 370 a.C., criou a Teoria das Proporções. Na linguagem matemática atual: a/b = c/d (“a está para b” assim como “c está para d”) se, e somente se, dados inteiros m e n então:
1) ma < nb se, e só se, mc < nd
2) ma = nb se, e só se, mc = nd
3) ma > nb se, e só se, mc > nb
Com esta definição de Eudoxo, passou a ser possível tratar
também de grandezas incomensuráveis, numa época em que não estavam definidos ainda os números irracionais.

Fração


Hipertexto
1. Texto feito para ser publicado na Internet com links para outros recursos disponibilizados pelo autor.
2. Texto que permite a navegação. Durante a leitura, o leitor desloca-se, designando, com a ajuda de um apontador situado no elemento onde se encontra, um elo ( ou link) que desencadeia a visualização de outros elementos.

Lema
Proposição auxiliar na demonstração de um teorema, que também precisa ser demonstrada.

Número
1. Elemento primitivo que não é definido;
2. A idéia de número nasceu dos processos de contagem e de medida.

Número Natural
Elemento primitivo que tem origem na contagem.

Número Racional
1.Todo número que pode ser representado na forma de fração.
2. Todo número que representa a medida de segmentos comensuráveis com a unidade.
3. Todo número que pode ser representado na forma decimal por decimais finitos (exatos) ou infinitos e periódicos.

Número Real
1.Todo número que representa a medida de um segmento. Para segmentos dotados de sentidos opostos, esta medida é dotada de um sinal (+) ou (-) para os diferentes sentidos.
2. Um número real pode ser racional ou irracional.

Número Irracional
1.Todo número real que não pode ser representado na forma de fração.
2. Todo número que representa a medida de segmentos incomensuráveis com a unidade.
3. Todo número que pode ser representado na forma decimal por decimais infinitos e não periódicos.

Número Irracional Algébrico
Todo número irracional que é raiz de um polinômio, como por exemplo, solução do polinômio x²– 2 = 0. Todos os irracionais representados por radicais são algébricos.

Número Irracional Transcendente
Todo número irracional que não é raiz de um polinômio, como por exemplo, e o número de Neper, e.

Número Complexo


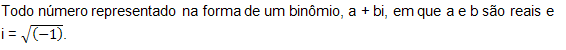
Medida
A medida de uma certa grandeza em relação a uma unidade padrão é o número que expressa o resultado da comparação da grandeza com a unidade.

Operação
Uma operação * num conjunto A é uma relação de um subconjunto do produto cartesiano AXA em A, tal que, a cada par ordenado deste subconjunto (x,y) associa um único elemento de A, x*y.

Uma operação é fechada se para todos os possíveis pares (x,y) de AxA sempre existe um corresponde x*y também em A.

Por exemplo, a adição é uma operação fechada no conjunto dos naturais pois a cada par de números (x,y) associa um único correspondente (x+y) que também é natural.

A subtração não é fechada no naturais porque só existe correspondente, também natural, para os pares ordenados (x,y) com a propriedade x > y.

Postulado
1. Princípios ou regras que não são demonstrados e que disciplinam a utilização dos conceitos primitivos e estabelecem suas propriedades.
2. Axiomas

Potenciação com base real e expoente inteiro

Princípio da Indução
Método de demonstração de proposições a respeito dos número naturais que consiste em provar que a proposição P(n) é válida para todos os números naturais n, se:
1) P(1) é válida
2) Se P(n) é válida então P(n+1) é válida.

Princípio da permanência
Princípio da analogia das definições e propriedades das operações do conjunto numérico A, num novo conjunto numérico B, que é considerado uma extensão de A.

Princípio da manutenção das operações formais e das propriedades já existentes, na construção de um novo conjunto.

Radiciação

Representações dos números racionais
Um número racional pode ser representado:
1) na forma fracionária (a/b, com a e b inteiros);

3) na forma percentual (P% = P/100)

Se e só se
1) Expressão que conecta duas afirmações consideradas equivalentes. A afirmação A é verdadeira se B é verdadeira e B é verdadeira se A é verdadeira.
2) Expressão que informa que duas frases P e Q são logicamente equivalentes.

Segmentos Comensuráveis

Segmentos incomensuráveis

Sistema decimal
O sistema decimal é um sistema de numeração de posição que utiliza a base dez. Os dez algarismos indo-arábicos - 0 1 2 3 4 5 6 7 8 9 - servem para contar unidades, dezenas, centenas, etc. da direita para a esquerda.

Sistema sexagesimal
O sistema sexagesimal é um sistema de numeração de base 60, criado pela antiga civilização Suméria. Uma possível razão para o aparecimento deste sistema de numeração poderá residir no elevado número de divisores de 60 (1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 e 60). Este sistema é utilizado nas medidas de ângulos (e de coordenadas geográficas angulares) e de tempo.

Teorema
Proposições matemáticas que são demonstradas, com base nos conceitos primitivos, nos axiomas, nas definições e em outros teoremas já demonstrados.

Webfólio
Ou portfólio, coleção de textos e outros recursos produzidos/ selecionados e organizados individualmente.
O webfolio propicia a revisão e avaliação contínua. O texto está sempre em aberto e o autor pode reformulá-lo, ao compreender melhor o tema de cada etapa, e dedicar-se simultaneamente à produção seguinte, aprimorando sempre, tendo em vista o produto final.